1 引言
旅行商问题(Traveling Salesman Problem,TSP)是一个经典的组合优化问题:说有一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。请问他应如何选择行进路线,以使总的行程最短?
旅行商问题的可行解是所有城市(假设数目为n)的全排列(n!)。随着城市数目的增加,可行解数目呈现指数增长,无法再多项式时间内穷举,因此TSP问题是一个非确定性多项式(Non-deterministic Polynomial )问题,也就是“NP”问题。由于较高的时间复杂度,“NP”问题规模较大时无法精确求解,因此只能寻求近似求解。
1997年,Dorigo等人[1]提出蚁群算法(Ant Colony System)并用于求解旅行商问题。蚁群算法受到“蚁群总是能以较短路线觅得食物”这一现象的启发。图1演示了这一过程:(a)中一些蚂蚁达到了分叉路口(一个决策点);(b)中一些蚂蚁选择了上方的路,另一些选择了下方的路;蚂蚁通常匀速前进并匀速释放信息素(Pheromone,用短虚线表示),(c)中选择更短路径的蚂蚁可以更快到达目标点,并且在路径上留下更浓密的信息素;(d)中越短的路径上留下了越多的信息素。后来的蚂蚁在路过相同的决策点是,有较大概率选择信息素浓度较高的路径,从而提升整个蚁群的觅食效率。
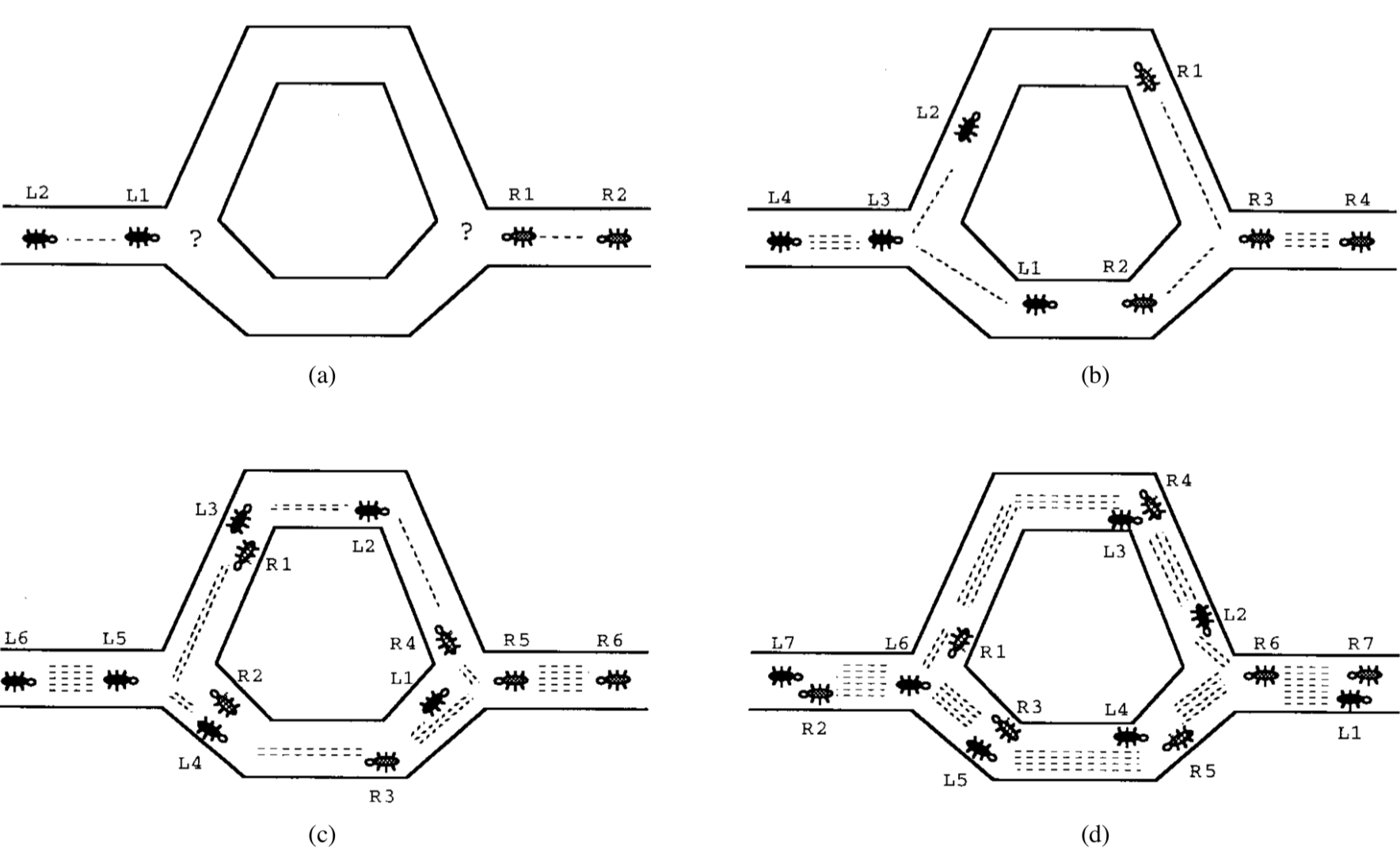
图1 蚁群行进策略演示
蚁群这这种智能优化方法如何通过形成算法和代码为我们所用呢?这就是本文要解决的问题。
2 方法
蚁群算法的流程是循环执行以下步骤,直到满足退出条件:
- 初始化蚁群参数。
- 蚁群中每只蚂蚁搜索一个可行解。
- 根据一次蚁群搜索的结果更新信息素。
- 判断是否终止与退出。
下面以求解旅行商问题为例,说明各个步骤。
2.1 初始化蚁群参数
在旅行商问题中,设城市的数量为n,城市i与j之间的距离为d_{ij}(i,j=1,2,\cdots,n)。
在蚁群算法中,设蚁群中蚂蚁数量为m,t时刻城市i与城市j路上的信息素浓度为\tau_{ij}(t)。初始时刻t=0时,各个城市之间连接路径上的信息素浓度相同,且为\tau_0,也就是\tau_{ij}(0)=\tau_0。
2.2 一只蚂蚁搜索可行解(转移概率建模)
蚁群中的蚂蚁k(k=1,2,\cdots,m)随机选择一个城市作为出发点,然后依概率随机选择下一个目标城市。设蚂蚁k在t时刻从城市i前往可达城市j的转移概率为P_{ij}^k(t),我们按如下思路建模:
- 根据蚁群的特性,转移概率
P_{ij}^k(t)应与城市之间的信息素浓度\tau_{ij}(t)正相关。这里假设成正比,即
P_{ij}^k(t) \propto \tau_{ij}(t) \tag{1}